第三章:简单逻辑门
复习
- 第一章:希望造出一台计算机。
- 第二章:这台计算机需要供能,输入,输出和处理过程。
TL;DR
- 晶体管可以搭建 and(与门)、or(或门)、not(非门)基础三门,进而搭建出 xor(异或门)等其他基础原件。
- 用 and 和 xor 可搭建出一个半加器。
- 两个半加器和一个与门可搭建出一个全加器。
- 多个全加器串联可搭建出一个串行进位加法器。
- 将串行进位加法器进行数字电路优化可以获得超前进位加法器。
正文
第二章末尾本应详细介绍冯·诺伊曼体系结构中的运算器和控制器,但此处暂缓,从第三章开始实现后,自然会理解这个结构,前两章为理论基础。既然要造计算机,肯定需要先能计算简单加减法。
基础材料
手头拥有的最基本材料为:电和晶体管(也可以使用电子管,但技术旧且效率低)。由第二章可知,此计算机采用二进制,与数学中布尔代数吻合。布尔代数为二进制信息表示和计算提供有力的数学支撑。
布尔代数有三种基本操作:and,or,not,分别是与门,或门,非门。其真值表如下表所示:
- 与门(输入均为 1 时才为 1,只要有 0 即为 0,“同真才真,其余均假”)
| 输入 A | 输入 B | 输出 Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
- 或门(输入只要有 1 就为 1,全为 0 即为 0,“有真就真,全假才假”)
| 输入 A | 输入 B | 输出 Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
- 非门(也称反相器,输入为 1 时输出为 0,输入为 0 时输出为 1,“真假对调”)
| 输入 | 输出 |
|---|---|
| 0 | 1 |
| 1 | 0 |
需要说明的是:与或非三种门,并不能直接获得,需要用晶体管搭建。但由于晶体管电路太过复杂,超出了本指南范围,本指南只将浅显解释附在其后,读者感兴趣可以自行阅读。
为简化说明,本指南 认为与或非三门可以直接获得。
由基础三门还可构成稍复杂一点的逻辑门:nand(not and 之缩写),nor(not or 之缩写),分别是与非门,或非门。其结果就是与门、非门的结果取反。
- 与非和或非
| 输入 A | 输入 B | and 输出 | nand 输出 | or 输出 | nor 输出 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 |
注意,nand 和 nor 两门因自身函数完备性,均可构成基础三门。所以一台计算机可以只由 nand 门或 nor 门构成。
半加器
接下来尝试计算一位加法(输出 Y 的括号为可能的进位):
| 输入 A | 输入 B | 输出 Y |
|---|---|---|
| 0 | 0 | (0)0 |
| 0 | 1 | (0)1 |
| 1 | 0 | (0)1 |
| 1 | 1 | (1)0 |
暂时不管进位,可以观察到:输入相同,结果为 0;输入不同,结果为 1。这种逻辑在以后也很常见,专门有个名字:异或门(xor)。
异或门电路可以使用基础三门搭建,方案也很多。总体来讲,用的逻辑门越少,开销越少,效率越高。下面两种设计方案中,很明显,第一种方案要好。
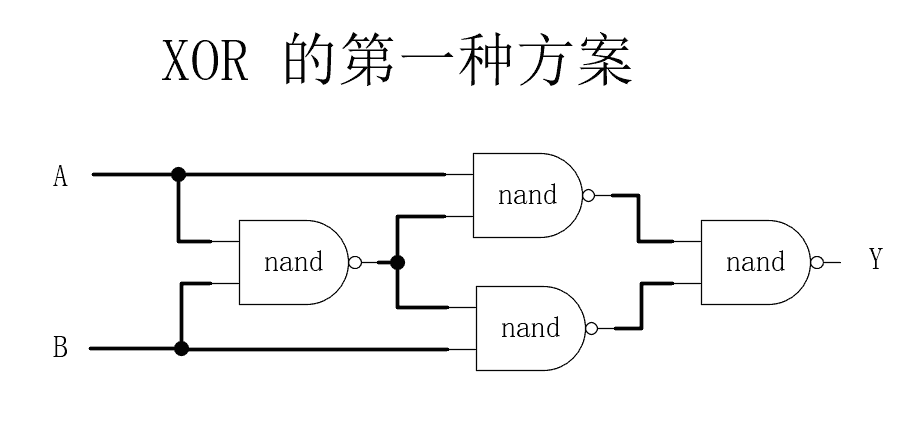
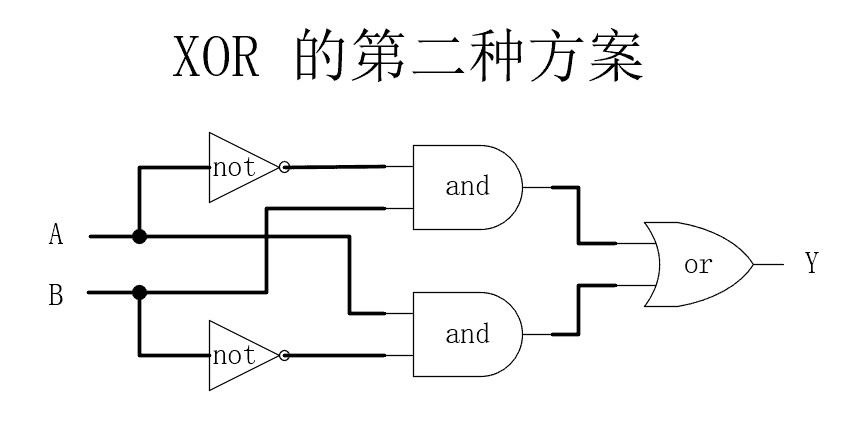
接下来处理棘手的进位问题:
再次观察,只有当输入均为 1 时才会出现进位,其他情况可以视为进位为 0。容易发现,此逻辑和与门相同:只有输入均为 1 时才为 1。
综上所述,二进制的一位加法器(带进位)可以用一个异或门加上一个与门表示。 将输入输出引脚分列两边,中间加上逻辑门,可以获得一个一位加法器。
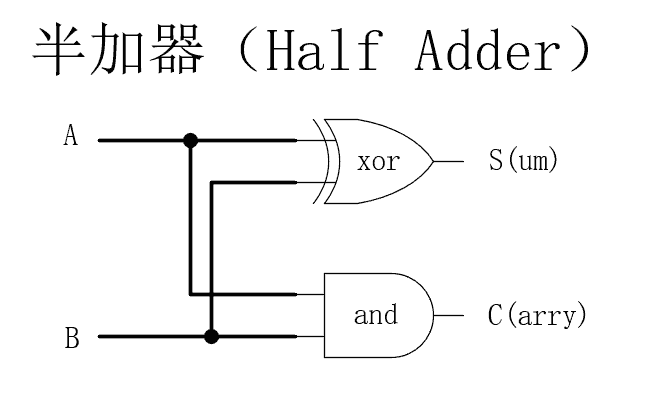
上述一位加法器也称半加器。
加法器(全加器)
来看一个例子,为简化问题,此处数据设为 4 位:计算 0011 + 1001。拆解为 4 个子问题,逐位相加,从左开始:0 + 1,0 + 0,1 + 0,1 + 1。可以观察到这四个问题可以用 4 个半加器解决。但是同时观察到,最后的子问题 1 + 1 产生了进位,所以还需要加上进位。
加上进位是个麻烦事。为了之后方便,可以将进位也直接纳入半加器电路,成为 3 输入 2 输出的一个全加器芯片。如图:
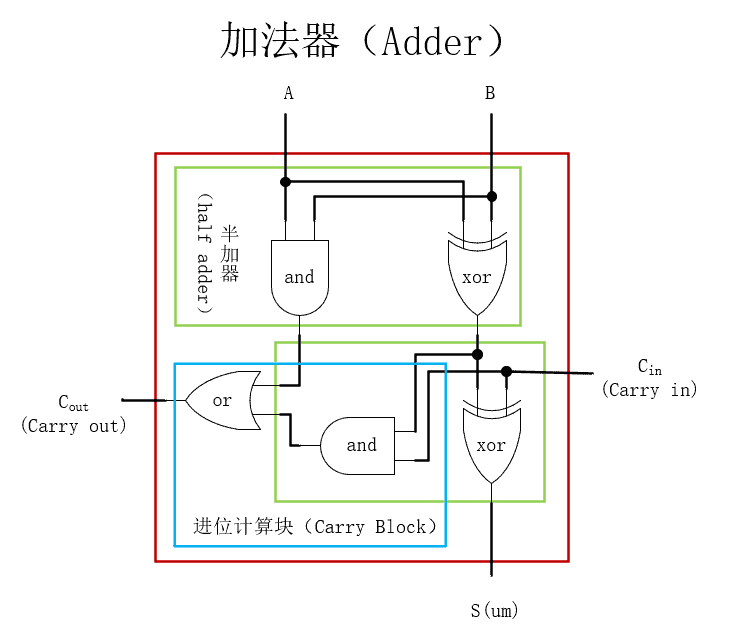
针对此例子可以画出如下电路图:
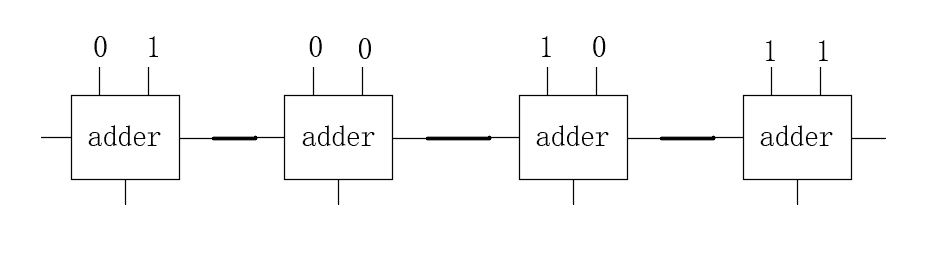
将问题泛化:计算 abcd + efgh(一个字母代表一个比特位)。产生 4 个子问题:a + e,b + f,c + g,d + h。因为不知道哪个问题会产生进位,所以均需要加上进位构成全加器,如图:
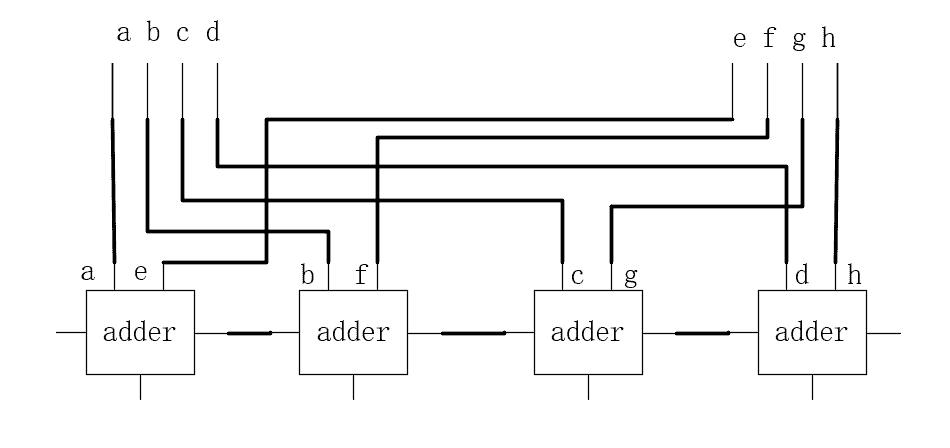
如果需要计算 8 位,将加法器扩展成 8 位的样子即可,16、32、64 位同理。
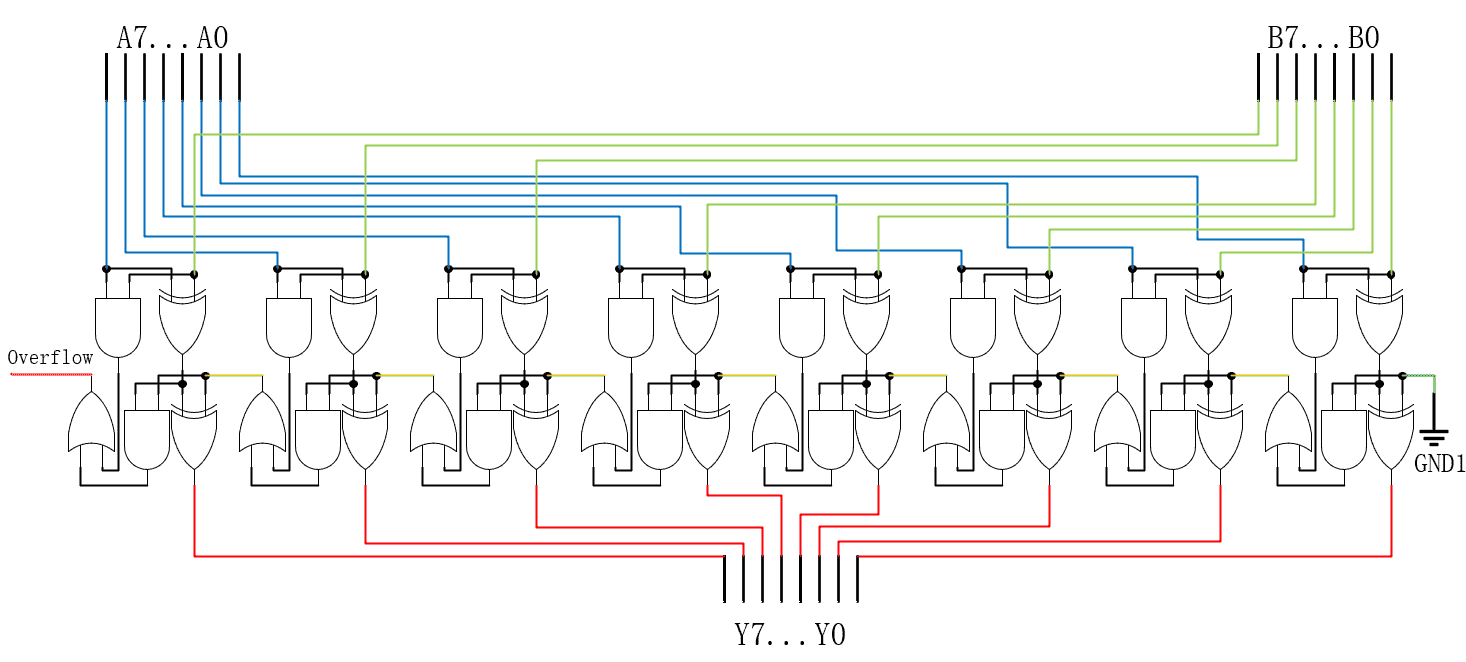
如果最高位(即二进制最左边的那一位)产生进位,代表超出了此计算机的数据范围。这里简单丢弃,后续再处理。
效率?
需要说明的是,将全加器直接串联起来构成的串行进位加法器(也称行波进位加法器),尤其懒惰和低效。现代电子所用的加法器,经过优化,速度更快。但无论如何,我们已经拥有加法器了。
本指南侧重如何构成加法器,不涉及加法器的优化,所以之后提到加法器时,默认已经过优化,效率比此章设计的加法器要高。
思考题
由于进位未知但不可缺少,每个全加器都要等待低位的进位,所以效率极低。
如果每个全加器耗时 0.1 秒,那么 8 位将耗时 0.8 秒。而现代 PC 基本都是 64 位,意味着做一次加法需要 6.4 秒。
有什么办法能优化这种速度吗?
补充
符号说明:
- NMOS 高于 阈值电压导通,低于 阈值电压不导通
- PMOS 则相反
- Vdd 为供电电压,恒为 1
- GND/Vss 为接地电压,恒为 0
- 接入端 A 和 B 为接入电压,可高可低,高于阈值电压为 1,低于阈值电压为 0
CMOS(互补式金属氧化物半导体)晶体管搭建基础逻辑门的电路图:
- 非门(反相器)
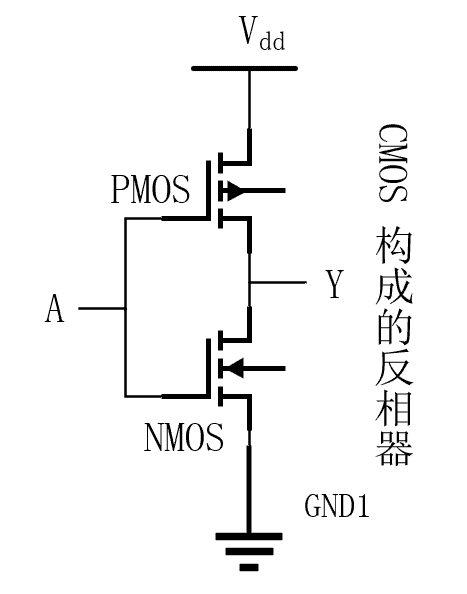
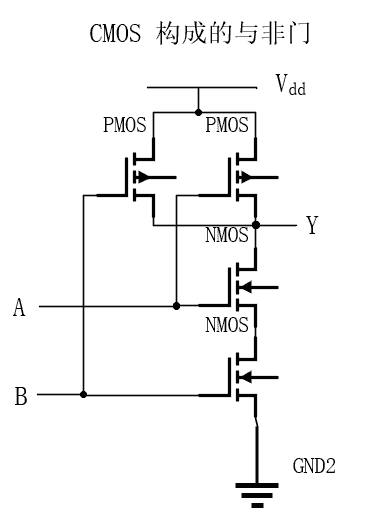
- 与非门
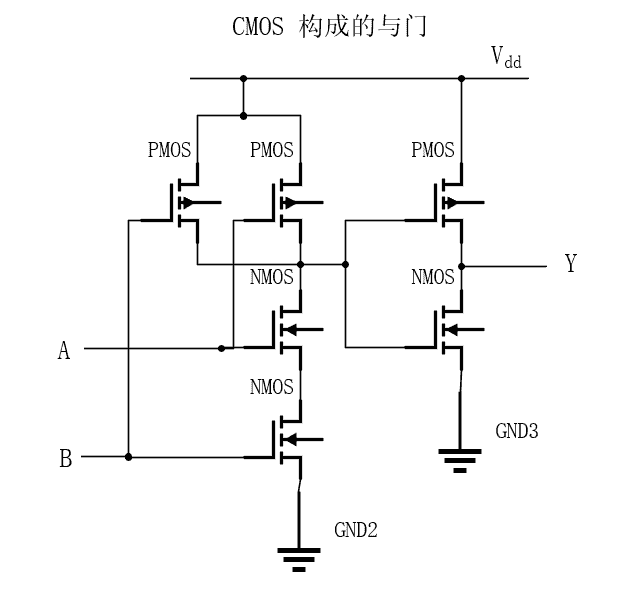
- 与门(可以看出实际上就是 nand + not 两模块构成)
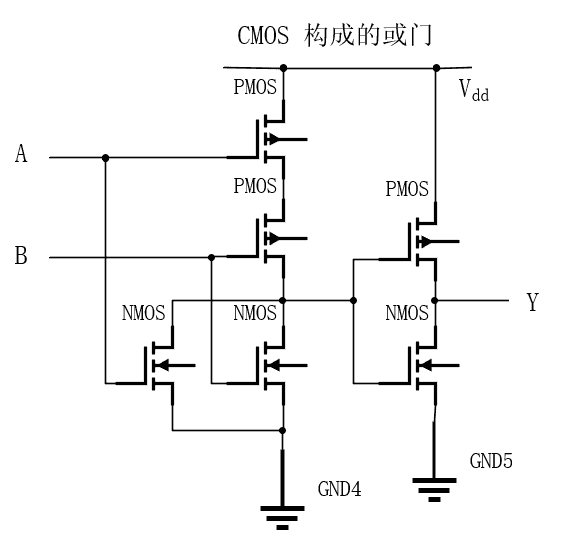
- 或门(与上同理,由 nor + not 构成)
小结
知识点
- 与门
- 或门
- 非门
- 半加器
- 全加器
- 加法器
参考资料
- Wikipedia(zh):晶体管:现代几乎所有电子设备的基石。
- Wikipedia(zh):函数完备性
- Wikipedia(zh):超前进位加法器:优化后的加法器,也有缺陷。
推荐
思考题答案(仅供参考)
可以使用超前进位加法器(也称并行进位加法器)。分析依赖关系之后,可以将进位从串联改为并联,能一定程度上提高效率。但当规模特别大时,此加法器会导致晶体管或逻辑门的数量指数级上升。需要数字电路知识。
协议
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。