第二章:计算机的构成
复习
- 第一章:需要一台计算机,在研究其组成的方向上进行努力。
TL;DR
- 使用 布尔代数(二进制数学基础) 和 电能(能源) ,设计出 输入设备、输出设备、存储单元和计算单元 ,就可以构成计算机。
- 四种组成部分可以继续向下向细拆分。例如计算单元可以由 CPU 拆成寄存器、ALU 和控制器等。
正文
供能
首先,要使机器工作:需要供能。目前最容易获取和广泛运用的能源:电能。
- 需要供电(能源)
处理
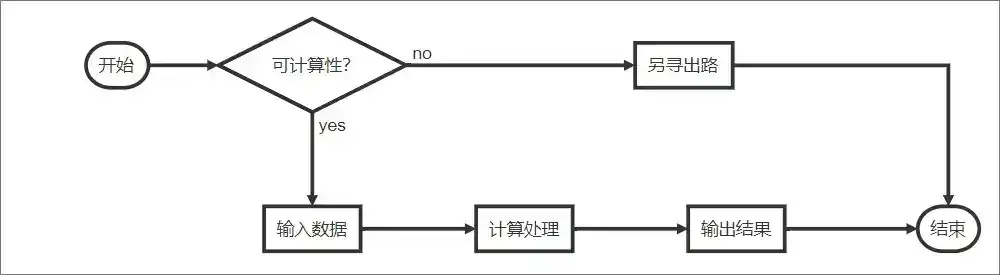
其次,计算,同处理事情的流程一样,需要:适用前提,已知条件和结果。由此,抽象出以下三点:
- 可计算性(适用前提)
- 输入数据(已知条件)
- 输出结果(结果结论)
内部表示
最后,考虑计算机内部计算处理的事情:
- 如何处理与计算机的交互?
- 信息和数据该怎么表示?
- 处理时会不会有中间结果,需不需要暂时保留?
交互处理
最初的计算机,只希望能快速计算。所以此处将问题最简化:能够输入数据就行。复杂交互处理不在考虑范围之内。
由于采用电能,所以最终一切都需要用电信号表示。电信号目前只能分为两种:通电,不通电。
我们需要区别这两种状态,并且,是在计算机一直供电的情况下,让计算机识别输入信号。
阻挡是一个办法。
最初的计算机科学家们,想到用纸带打孔。有孔洞,类似开关,电路接通,通电。没有孔洞,电路受阻,不通电。如下图:
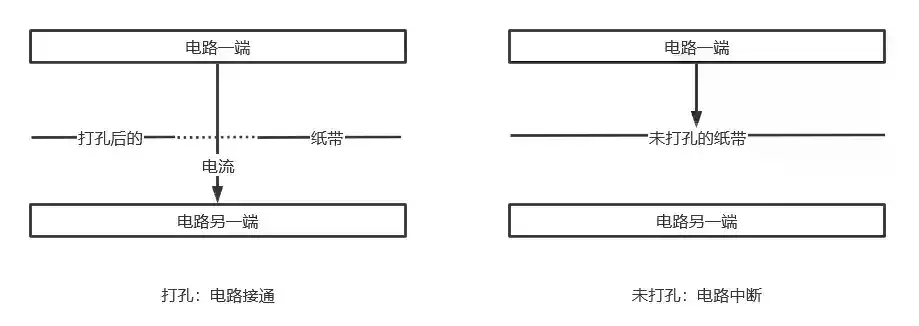
这就是最原始的方法,需要程序员做大量的打孔操作,让机器识别。
数据表示
由于交互处理的前提,需要将所有信息都用通电和不通电表示。
假设
- 通电表示 a,不通电表示 b。那其他字母怎么办呢?行不通。
- 通电表示 1,不通电表示 0。那其他数字怎么办呢?似乎可以。
玛雅人采用 20 进制;我们日常使用 10 进制;有些单位(一打)使用 12 进制。
那么是否可以采用 2 进制?逢 2 进 1,将其他数字表示出来?
| 二进制 | 十进制 | 二进制 | 十进制 |
|---|---|---|---|
| 0000 | 0 | 0101 | 5 |
| 0001 | 1 | 0110 | 6 |
| 0010 | 2 | 0111 | 7 |
| 0011 | 3 | 1000 | 8 |
| 0100 | 4 | 1001 | 9 |
回到假设 1:如果需要表示字母和其他符号,怎么办?进制只能表示数字。
既然数字这个界限不能打破,那么是否可以抽一部分数字出来,专门用来表示其他字母或者符号?美国想出了这个方法,由此诞生 ASCII 码。详细了解请见参考资料。
思考题 1
这个方法似乎也有些问题。例如,ASCII 码中规定 0100 0001(二进制,转换为十进制为 65)表示字母 A ,那真要表示 65 怎么办?以及,上述的假设 1,其他字母真的就表示不出来吗?
这个方法可以解决问题。虽不完美,但目前没有想出更好的解决办法,就这样先用着。
为了方便计算机学界交流,为这些知识起个术语:
- 一个二进制的 0 或 1 称为 bit,比特,用 b 表示
- 8 个二进制的 0 或 1 成为 Byte,字节,用 B 表示
- 8 是人为规定的,二进制表示一个数据会非常长,表示 0-9 都需要 4 个 bit
中间结果
毋庸置疑,需要保存中间结果。原因:
- 我们希望一次性将所有计算任务都输入进去,等待计算机完成。而非计算一次输入一次。
- 计算较为复杂时,中间结果不可丢弃,否则后续计算将出现错误。
我们需要有某个东西,能够存放数据,即存放中间结果的二进制表示。我们姑且称为“存储器”。
体系结构
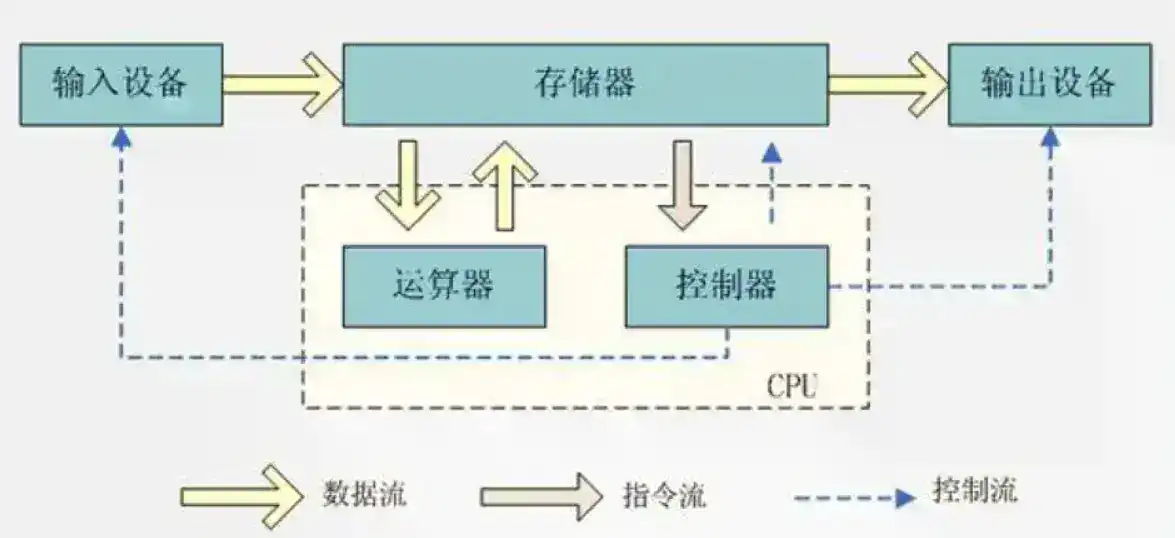
处理完三个棘手的问题,得出新的结论,一台计算机需要有:
上述体系结构,被称为冯·诺依曼体系结构,至今仍在沿用(人类所有知识都来源于好奇心和解决问题)。如图所示:
思考题 2
如果未来发生了一场能源革命,发现一种新能源:另能。另能激活时,有 A、B、C 三种不同的形态,均可导通另路(类似电路)。
那么计算机是否会发生革命?如果你是另能计算机设计者,会采用几进制?
最后,冯·诺伊曼体系结构是否会随着技术发展而打破?
小结
知识点
一个核心:计算机如何构成。达成这个目的,需要:
- 能源
- 输入
- 输出
- 计算处理
- 二进制和 ASCII 码
- 比特(bit)
- 字节(Byte)
- 存储器
- 计算单元
- 二进制和 ASCII 码
- 冯·诺伊曼体系结构
参考资料
-
计算理论:一个问题是否可以计算。偏数学领域,不在讨论范围之内。
-
ASCII 码:American Standard Code for Information Interchange,美国信息交换标准代码。
-
二进制:数据的表示方法。
-
冯·诺依曼体系结构:现代电子计算机的基本体系结构。
-
Сетунь:苏联诞生的三进制计算机。
思考题答案(仅供参考)
思考题 1
-
65 和 A 的表示原理相同。A 是一个字符,65 是 6 和 5 两个字符。表示 65,即表示 6 的 ASCII 代码,然后跟上 5 的 ASCII 代码:0011 0110(6) 0011 0101(5)。注意:此处只讨论这两个字节用于显示,而非用于计算或表示指令等。
-
可以用 a 和 b 进行进制排列。如 a 表示 a,b 表示 b,ba 表示 c,bb 表示 d,baa 表示 e,bab 表示 f,bba 表示 g 等。但此方法实质一样,并且违背现存符号体系,不采用。如果不采用进制排列,因元符号(不可再分的符号单位)只有通电与不通电,所以只能表示两个信息。目前没有突破采用进制以外的信息表示法(符号少,只能依靠排列增加信息数量)。
请注意:此答案 2 并不严谨,但于初学者而言,容易理解且偏差不大。(苏联曾经诞生过三进制计算机)
思考题 2
- 会。因为元符号数量从 2 个增长为 4 个。
- 4 进制。未导通态 1 个加上导通态 3 个,共 4 个。可以表示为 0-3,此时每 1 位(四进制)可以表示 2 个比特位(二进制)。
- 科学和技术一直在进步。假设,某一天技术强大到所有输入和输出均可一个设备完成,则该体系也会随之淘汰。
协议
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。